
La Thuile Ski Extreme Black 3, originally uploaded by Me (?).
I have just come back from an excellent skiing holiday in La Thuile, Italy. A great range of slopes and for the most part of the holiday great snow.
One of the highlights of La Thuile is two black runs that come down the right hand side of the mountain. The imaginatively named "Black 2" and "Black 3". We spent most of the week going down Black 2 a few times a day as it was challenging enough but not too hard. One highlight of Black 2 was the last stretch that we dubbed "the ski jump" as it was very steep and if you got there early enough in the day you can schuss all the way down from the top.
I actually invented a new style of skiing on Black 2 ski jump, I call it "back surfing". It was not technically skiing as such as it involved going down the slope head first on my back with my skis in the air! I had decided to put in one last turn before schussing and lost my balance. I ended up on my back going down the steep slope, in order that I did not have to face a walk back up to retrieve any skis that came off I put my feet in the air to stop the skis catching and coming off. This had the interesting effect of stopping all braking and I ended up coming all the way down on my back. When I stopped laughing I stood up and carried on!
Whilst we did Black 2 quite a few times we were put off by Black 3 by the sign at the top that indicated the steepest part was 73% and that the run featured in world cup skiing events. Eventually we plucked up courage on our last day and Chris, Pat and I headed down Black 3. It was steep but not as steep as we had imagined it would be.
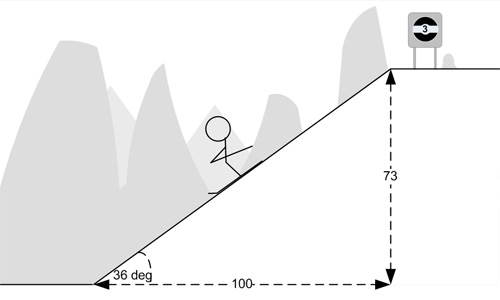
When we got back, Pat pointed out that a 100% gradient was only 45 degrees and so therefore a 73% gradient was only 36 degree slope. So there started the mystery: Just how steep is a 73% slope...?
Theory 1 – Height change by vertical distance
Theory 2 – Vertical distance by height change
In desperation I decided they must have measured it wrong and so decided to swap the lengths over. This makes the angle of the slope 56 degrees. This is certainly more "ski extreme" but I cannot find any evidence of anyone ever measuring a slope this way round.
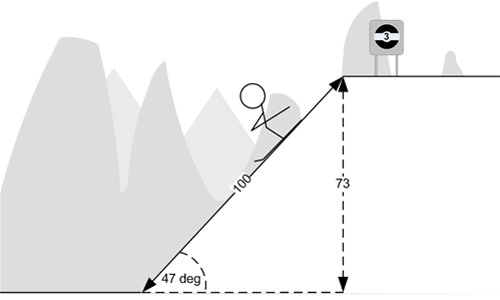
Theory 3 – Height change by distance travelled
Looking for additional help I remembered about the UK La Thuile fan site LaThuile.co.uk. On the site it says:
"If you have any questions about La Thuile then email and we'll see if we can help."
So I thought it is worth a go and sent an email off. A few days later I got an excellent email from Woody the site owner with some text from a site about road gradients for cyclists. The site took a bit of time to get my head round it, but it says that road gradients are sometimes measured by the distance travelled by the height change. How you tell the difference I don't know!
Using the sohcahtoa mnemonic from school the angle of the slope is the arcsine of the opposite over the hypotenuse. So this makes our angle 47 degrees.
Looking at the scale diagram that looks more realistic but it does not look that steep either.
So, I am still none the wiser - I suspect that theory 3 is correct though it still does not look as steep as I remember it. I have emailed off to the La Thuile visitor information people but am still waiting for a reply.
I know this, next time I go skiing I am taking some sort of GPS with me!
Here is the Black 3 subset of the extreme ski team: Chris, me & Pat.





No comments:
Post a Comment